Math Portal
Introductory Statistics
Section 2.2 - Permutations
A permutation is an ordered arrangement of a set of distinctly different items. For example, two permutations of the numbers one through five are 12345 and 53142. For permutations, different orderings of the same items are counted as distinctly different permutations. Thus, when the order of the items in an arrangement is important in a problem, you have a permutation problem.
Through a direct application of the Fundamental Counting Principle, the number of permutations of n distinct items is given by: n! = n(n-1)(n-2)(n-3)...(2)(1) where the notation n! is read n factorial.
A factorial is the product of all positive integers less than or equal to a given positive integer. Exception: By definition 0! = 1.
Sometimes, when you have n items, you might want to count the number of different possible arrangements of some, instead of all, of the items. The number of permutations of r items selected from n distinctly different items is denoted by n Pr and is equal to
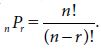
When you apply the formula n Pr, you need to make sure that (1) the n items from which you select are n mutually different items (that is, none are alike), (2) the r items that you select from the n items are selected without replacement, and (3) different orderings of the same r items are counted separately.
EXAMPLE: Six separate people are to be seated in four chairs that are placed in a straight row. How many different arrangements of the six people in the four chairs are possible?
SOLUTION: Since the order in which the people are seated is important, this is a permutation problem. The number of different possible arrangements of the six people in the four chairs is given by

When you want to count the number of different possible arrangements of n items, but some of the n items are identical to each other, you use a formula that adjusts for the like items. You simply divide by the number of permutations that are identical as shown by
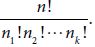
EXAMPLE: How many different ways can you arrange the six letters in the word banana if you use all six letters each time?
SOLUTION: Since the order in which the letters appear is important, this is a permutation problem. The word banana consists of six letters: one b, three a’s, and two n’s. Since the six items to be arranged are not all mutually different items, the number of arrangements is given by
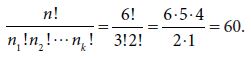
Some situations that indicate you might have a permutation problem are the following: creating codes, passwords, or license plates; making words; assigning roles; filling positions; making ordered arrangements of things (people, objects, colors, and so on); selecting persons or things as first, second, third, and so on; flipping several coins and observing head or tail on each coin; distributing items among several objects or people; and similar situations.
A permutation is an ordered arrangement of a set of distinctly different items. For example, two permutations of the numbers one through five are 12345 and 53142. For permutations, different orderings of the same items are counted as distinctly different permutations. Thus, when the order of the items in an arrangement is important in a problem, you have a permutation problem.
Through a direct application of the Fundamental Counting Principle, the number of permutations of n distinct items is given by: n! = n(n-1)(n-2)(n-3)...(2)(1) where the notation n! is read n factorial.
A factorial is the product of all positive integers less than or equal to a given positive integer. Exception: By definition 0! = 1.
Sometimes, when you have n items, you might want to count the number of different possible arrangements of some, instead of all, of the items. The number of permutations of r items selected from n distinctly different items is denoted by n Pr and is equal to
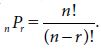
When you apply the formula n Pr, you need to make sure that (1) the n items from which you select are n mutually different items (that is, none are alike), (2) the r items that you select from the n items are selected without replacement, and (3) different orderings of the same r items are counted separately.
EXAMPLE: Six separate people are to be seated in four chairs that are placed in a straight row. How many different arrangements of the six people in the four chairs are possible?
SOLUTION: Since the order in which the people are seated is important, this is a permutation problem. The number of different possible arrangements of the six people in the four chairs is given by

When you want to count the number of different possible arrangements of n items, but some of the n items are identical to each other, you use a formula that adjusts for the like items. You simply divide by the number of permutations that are identical as shown by
EXAMPLE: How many different ways can you arrange the six letters in the word banana if you use all six letters each time?
SOLUTION: Since the order in which the letters appear is important, this is a permutation problem. The word banana consists of six letters: one b, three a’s, and two n’s. Since the six items to be arranged are not all mutually different items, the number of arrangements is given by
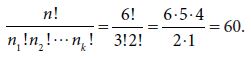
Some situations that indicate you might have a permutation problem are the following: creating codes, passwords, or license plates; making words; assigning roles; filling positions; making ordered arrangements of things (people, objects, colors, and so on); selecting persons or things as first, second, third, and so on; flipping several coins and observing head or tail on each coin; distributing items among several objects or people; and similar situations.