Math Portal
Introductory Statistics
Section 2.3 - Combinations
A combination is an arrangement of a set of distinct items in which different orderings of the same items are considered the same. For example, the set of vowels a, e, i, o, and u is the same as the set of vowels i, a, u, o, and e. That is, in a combination problem (unlike a permutation problem), different orderings of the same items are not counted as separate results. Thus, when the order in which the items are arranged is not important in the problem, you have a combination problem. The number of combinations of r items selected from n distinct items is denoted by n C r and is equal to
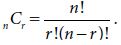
EXAMPLE: How many different ways can a club of 25 members select a 3-member officer nominating committee from its membership if all members are eligible to serve on the committee?
SOLUTION: Since the order in which the committee members are arranged is not important in the problem, this is a combination problem (If order mattered it would be a permutation problem. The number of different possible 3-member committees that can be formed from the 25 club members is given by

When you apply the formula n C r, you need to make sure that
EXAMPLE: A shopper will buy 6 shirts, 3 pairs of slacks, and 2 pairs of shoes from a selection of 10 different shirts, 7 different pairs of slacks, and 5 different pairs of shoes. How many different ways can the shopper make the purchase?
SOLUTION: Thinking in terms of the Fundamental Counting Principle, the shopper has three tasks to do: Select 6 of the 10 shirts, select 3 of the 7 pairs of slacks, and select 2 of the 5 pairs of shoes. Since the order of selection of the clothing items is not important in the problem, the number of ways to select each of the clothing items can be determined using the combination formula. Then, following those calculations, the Fundamental Counting Principle can be used to determine the total number of different ways the shopper can make the purchase. Thus, the number of different ways the shopper can make the purchase equals (the number of ways to select 6 of 10 shirts) x (the number of ways to select 3 of 7 pairs of slacks) x (the number of ways to select 2 of 5 pairs of shoes) = 10 C 6 x 7 C 3 x 5 C 2 =

Some situations that indicate you might have a combination problem are the following: making a collection of things (books, coins, and so on), selecting a committee, choosing questions from a test, counting the number of subsets of a given size from a set, dealing hands from a deck of cards, selecting pizza toppings, listing the combinations from a set of items, choosing students for groups, and similar situations.
A combination is an arrangement of a set of distinct items in which different orderings of the same items are considered the same. For example, the set of vowels a, e, i, o, and u is the same as the set of vowels i, a, u, o, and e. That is, in a combination problem (unlike a permutation problem), different orderings of the same items are not counted as separate results. Thus, when the order in which the items are arranged is not important in the problem, you have a combination problem. The number of combinations of r items selected from n distinct items is denoted by n C r and is equal to
EXAMPLE: How many different ways can a club of 25 members select a 3-member officer nominating committee from its membership if all members are eligible to serve on the committee?
SOLUTION: Since the order in which the committee members are arranged is not important in the problem, this is a combination problem (If order mattered it would be a permutation problem. The number of different possible 3-member committees that can be formed from the 25 club members is given by

When you apply the formula n C r, you need to make sure that
- the n items from which you select are n distinct items
- the r items that you select come from the n items and are selected without replacement
- different orderings of the same r items are not distinguished as being different from each other.
EXAMPLE: A shopper will buy 6 shirts, 3 pairs of slacks, and 2 pairs of shoes from a selection of 10 different shirts, 7 different pairs of slacks, and 5 different pairs of shoes. How many different ways can the shopper make the purchase?
SOLUTION: Thinking in terms of the Fundamental Counting Principle, the shopper has three tasks to do: Select 6 of the 10 shirts, select 3 of the 7 pairs of slacks, and select 2 of the 5 pairs of shoes. Since the order of selection of the clothing items is not important in the problem, the number of ways to select each of the clothing items can be determined using the combination formula. Then, following those calculations, the Fundamental Counting Principle can be used to determine the total number of different ways the shopper can make the purchase. Thus, the number of different ways the shopper can make the purchase equals (the number of ways to select 6 of 10 shirts) x (the number of ways to select 3 of 7 pairs of slacks) x (the number of ways to select 2 of 5 pairs of shoes) = 10 C 6 x 7 C 3 x 5 C 2 =
Some situations that indicate you might have a combination problem are the following: making a collection of things (books, coins, and so on), selecting a committee, choosing questions from a test, counting the number of subsets of a given size from a set, dealing hands from a deck of cards, selecting pizza toppings, listing the combinations from a set of items, choosing students for groups, and similar situations.