Math Portal
Introductory Statistics
Section 2.5 - Classical Probability
A probability on a sample space, S, is a function that assigns to each outcome in S a real number between 0 and 1, inclusive. The sum of the probabilities of all of the outcomes should equal 1. For instance, for S = {1, 2, 3, 4, 5, 6}, the sample space for the experiment of tossing a fair die one time and observing the up face, the probability of each outcome in S is 1 out of 6 (1/6)(since each number has an equal chance of showing on the up face). The sum of the probabilities of the outcomes in S is P(1)+P(2)+P(3)+P(4)+P(5)+P(6) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1, where P(1) is the probability that you roll a 1, P(2) is the probability that you roll a 2, etc.
An event, E, is a collection of outcomes from a sample space S; that is, an event E is a subset of the sample space S. An event E is said to occur if a member of E occurs when the experiment is performed. For example, if the sample space is the set of outcomes from the experiment of tossing a fair die and observing the up face, and E is the event that the die shows a number less than 3, then S = {1, 2, 3, 4, 5, 6} and E = {1, 2}.
The probability of an event E, denoted P(E), is the sum of the probabilities of the individual outcomes that are members of the event E. The probability of an event is a numerical value between 0 and 1, inclusive, that quantifies the chance or likelihood that the event will occur. For instance, given the sample space S = {1, 2, 3, 4, 5, 6}, the set of outcomes from the die tossing experiment, and E = {1, 2}, the event that the die shows a number less than 3, you have P(E)=P(1)+P(2) = 1/6 + 1/6 = 2/6 = 1/3.
Outcomes are equally likely if each outcome has the same chance to occur, in other words their probabilities are the same. If all outcomes in the sample space are equally likely, the probability of an event E is given by:
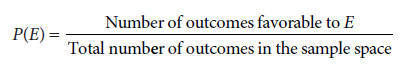
For example, for the die-tossing experiment and the event E that the die shows a number less than 3,

When using the formula for the probability of an event, the denominator always will be larger than or equal to the numerator, so check for this when you plug into the formula. Probabilities can be expressed as fractions, decimals, or percents.
Keep in mind that the formula for probability in which the outcomes are equally likely will not apply to sample spaces in which the events are not equally likely. For instance, the sample space for spinning a spinner that is one-fourth red, one-fourth yellow, and one-half green is S = {R, Y, G}, where R means the spinner lands on red, Y means the spinner lands on yellow, and G means the spinner lands on green. The probabilities for the three different outcomes are the following:

An event is certain to occur if and only if the probability of the event is 1. An event is impossible if and only if the probability of the event is 0. The probability of any event is a number between 0 and 1, inclusive. Thus, the lowest probability you can have is 0, and the highest probability you can have is 1. All other probabilities fall between 0 and 1. The closer the probability of an event is to 1, the more likely the event is to occur; the closer the probability of an event is to zero, the less likely the event is to occur.
A probability on a sample space, S, is a function that assigns to each outcome in S a real number between 0 and 1, inclusive. The sum of the probabilities of all of the outcomes should equal 1. For instance, for S = {1, 2, 3, 4, 5, 6}, the sample space for the experiment of tossing a fair die one time and observing the up face, the probability of each outcome in S is 1 out of 6 (1/6)(since each number has an equal chance of showing on the up face). The sum of the probabilities of the outcomes in S is P(1)+P(2)+P(3)+P(4)+P(5)+P(6) = 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1, where P(1) is the probability that you roll a 1, P(2) is the probability that you roll a 2, etc.
An event, E, is a collection of outcomes from a sample space S; that is, an event E is a subset of the sample space S. An event E is said to occur if a member of E occurs when the experiment is performed. For example, if the sample space is the set of outcomes from the experiment of tossing a fair die and observing the up face, and E is the event that the die shows a number less than 3, then S = {1, 2, 3, 4, 5, 6} and E = {1, 2}.
The probability of an event E, denoted P(E), is the sum of the probabilities of the individual outcomes that are members of the event E. The probability of an event is a numerical value between 0 and 1, inclusive, that quantifies the chance or likelihood that the event will occur. For instance, given the sample space S = {1, 2, 3, 4, 5, 6}, the set of outcomes from the die tossing experiment, and E = {1, 2}, the event that the die shows a number less than 3, you have P(E)=P(1)+P(2) = 1/6 + 1/6 = 2/6 = 1/3.
Outcomes are equally likely if each outcome has the same chance to occur, in other words their probabilities are the same. If all outcomes in the sample space are equally likely, the probability of an event E is given by:
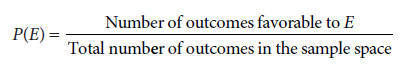
For example, for the die-tossing experiment and the event E that the die shows a number less than 3,
When using the formula for the probability of an event, the denominator always will be larger than or equal to the numerator, so check for this when you plug into the formula. Probabilities can be expressed as fractions, decimals, or percents.
Keep in mind that the formula for probability in which the outcomes are equally likely will not apply to sample spaces in which the events are not equally likely. For instance, the sample space for spinning a spinner that is one-fourth red, one-fourth yellow, and one-half green is S = {R, Y, G}, where R means the spinner lands on red, Y means the spinner lands on yellow, and G means the spinner lands on green. The probabilities for the three different outcomes are the following:
An event is certain to occur if and only if the probability of the event is 1. An event is impossible if and only if the probability of the event is 0. The probability of any event is a number between 0 and 1, inclusive. Thus, the lowest probability you can have is 0, and the highest probability you can have is 1. All other probabilities fall between 0 and 1. The closer the probability of an event is to 1, the more likely the event is to occur; the closer the probability of an event is to zero, the less likely the event is to occur.