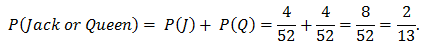Math Portal
Introductory Statistics
Section 2.7 - The Addition Rule for Probability
A compound event is a combination of two or more events. For two events A and B, a compound event that is important in probability is the compound event A or B. Note that in mathematics, the word or is used in the inclusive sense. Therefore, the compound event A or B is the event that A occurs or B occurs or that both occur simultaneously on one trial of an experiment.
The addition rule states that P(A or B) = P(A) + P(B) - P(A and B) (they occur simultaneously). Keep in mind that this rule applies to one trial of an experiment.
EXAMPLE: Suppose one card is drawn at random from a standard deck of 52 playing cards; find the probability that the card is a jack or a diamond.
SOLUTION: There are 4 jacks in the deck, so P(jack) = 4/52. There are 13 diamonds, so P(diamond) = 13/52. There is one jack of diamonds card, so P(jack and diamond occur simultaneously) = 1/52. Thus, P(jack or diamond) = P(jack) + P(diamond) - P(jack and diamond)
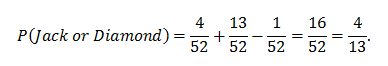
Two events are mutually exclusive if they cannot occur at the same time; that is, they have no outcomes in common. For instance, if you randomly draw one card from a deck of cards, the event of drawing a red card and the event of drawing a club are mutually exclusive.
When two events A and B are mutually exclusive, P(A or B) = P(A) + P(B).
EXAMPLE: One card is randomly drawn from a well-shuffled standard deck of 52 playing cards. Find the probability that the card drawn is a jack or a queen.
SOLUTION: There are four jacks in the deck, so P(J) = 4/52. There are four queens in the deck, so P(Q) = 4/52. The event of drawing a queen and the event of drawing a jack are mutually exclusive (since you cannot draw both at the same time on one draw from the deck), so
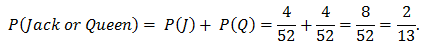
A compound event is a combination of two or more events. For two events A and B, a compound event that is important in probability is the compound event A or B. Note that in mathematics, the word or is used in the inclusive sense. Therefore, the compound event A or B is the event that A occurs or B occurs or that both occur simultaneously on one trial of an experiment.
The addition rule states that P(A or B) = P(A) + P(B) - P(A and B) (they occur simultaneously). Keep in mind that this rule applies to one trial of an experiment.
EXAMPLE: Suppose one card is drawn at random from a standard deck of 52 playing cards; find the probability that the card is a jack or a diamond.
SOLUTION: There are 4 jacks in the deck, so P(jack) = 4/52. There are 13 diamonds, so P(diamond) = 13/52. There is one jack of diamonds card, so P(jack and diamond occur simultaneously) = 1/52. Thus, P(jack or diamond) = P(jack) + P(diamond) - P(jack and diamond)
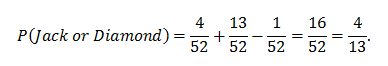
Two events are mutually exclusive if they cannot occur at the same time; that is, they have no outcomes in common. For instance, if you randomly draw one card from a deck of cards, the event of drawing a red card and the event of drawing a club are mutually exclusive.
When two events A and B are mutually exclusive, P(A or B) = P(A) + P(B).
EXAMPLE: One card is randomly drawn from a well-shuffled standard deck of 52 playing cards. Find the probability that the card drawn is a jack or a queen.
SOLUTION: There are four jacks in the deck, so P(J) = 4/52. There are four queens in the deck, so P(Q) = 4/52. The event of drawing a queen and the event of drawing a jack are mutually exclusive (since you cannot draw both at the same time on one draw from the deck), so