Teens At Work

A. My population of interest is juniors and seniors. My sample size is 80 students.

To randomly select my samples, I put all the names of juniors and seniors in the Minitab Lab worksheet. Then I went to Calc-Random Data-Sample from columns. I put in 80 for Sample, C1 and C2 in rows from column(s), and C1 and C2 in store samples in. Then I went to Manip-Sort, putting in C1 (last names) and C2 (first names) in Sort Columns. Then I put C1 in Sort by column since I only need to sort out the last names of the samples. After the sorting, I print out the names of the 80 students and went to the guidance office. I wrote down the names of each student and his/her teacher (any teacher) name and the period with that teacher on a sticky note. After that I put the sticky notes on the survey shown below. I sort out the teachers’ last names so that Mrs. Caso will put them in the teacher mailboxes. 

Survey:

LV

Please respond to the following:

 

Grade:    11       12

Gender: M     F

Are you currently working on a job?    Yes       No

  

π ₁ : The proportion of working male NOHS students

π₂ : The proportion of working female NOHS students

Ho: π ₁ = π₂      

Ha:  π ₁ ≠ π ₂

a = 0.05

Assumptions:

            The samples are independent random samples.

            The distributions for males and females are assumed normal.

            Distribution is approximated normal by:

            n π 1≥10                      14(11/14) ≥10

            n(1- π 1) ≥10               14(1-11/14) ≤10

            n π 2≥10                      23(17/23) ≥10

            n(1- π 2) ≥10               23(1-17/23) ≥10

       

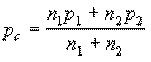
Test and CI for Two Proportions

Sample X N Sample p

1 11 14 0.785714

2 23 40 0.575000

Estimate for p(1) - p(2): 0.210714

95% CI for p(1) - p(2): (-0.0532312, 0.474660)

Test for p(1) - p(2) = 0 (vs not = 0): Z = 1.56 P-Value = 0.118

* NOTE * The normal approximation may be inaccurate for small samples.

 

Z= 01.56

P-value= 0.118