The study...

For our significance test we chose to use a two sample t-test to infer if the means are different. The assumptions were met as the samples were independently chosen and the sample size is > 30 so the CLT applies.

µ1 = mean weight of girl’s purses who don’t carry food.

Ho:   µ1 -  µ2 = 0

Ha:   µ1 -  µ2 < 0

α = 0.05

Assumptions: Both samples were independently selected and the sample sizes are both over 30 indicating that the CLT applies.

t = = -2.2817

Results for: data.HTM

 Two-Sample T-Test and CI: Weight, Food
Two-sample T for Weight
Food   N  Mean  StDev  SE Mean
N     29  4.24   2.33     0.43
Y     47  5.36   1.60     0.23

 Difference = mu (N) - mu (Y)
Estimate for difference:  -1.124
95% upper bound for difference:  -0.297
T-Test of difference = 0 (vs <): T-Value = -2.28  P-Value = 0.014  DF = 44

p-value = .013674

Conclusion: We reject the null hypothesis at the 0.05 level of significance because the p-values < α. Therefore, there is sufficient evidence to say that the true mean of girl’s purse weight whom carry food is greater than the mean purse weight of girls who don’t carry food.

 
 

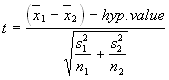-DATA

-GRAPHS