Sampling
In order to obtain our
data, we used a stratified random sampling method. We took every
single NOHS varsity fall sports participant and put there name into
Minitab. We also took every single NOHS varsity winter sports
participant and put there name into Minitab as well. Using a random
sample generator, we had Minitab select 60 random names for each
sample. Hence, in each of the two
samples that we obtained, 60 people were obtained. We went and
weighed as many of them as they allowed, hoping to at least obtain a
30 people from each sample, in order for the population to be
approximately normal, as according to the Central Limit Theorem. We
knew we would get some non-response bias because of the fact that we
are physically weighing the people, and some people may not be okay
with that.
HYPOTHESIS TEST
For our hypothesis test we chose to use a 2 sample t-test since we are using both fall and winter athletes which are obtained from two independent random samples. We are trying to determine if there is a difference between the weights of fall and winter varsity athletes at North Olmsted High School. Our null hypothesis is that both fall and winter sports athletes have an equal average weight. Our alternative hypothesis is that fall varsity athletes at NOHS have a greater average weight than winter varsity athletes at NOHS.
SIGNIFICANCE TEST
U1=The true mean weight of varsity fall athletes at North Olmsted High School
U2= The true mean weight of varsity winter athletes at North Olmsted High School
Ho: U1=U2 Ha: U1>U2 α= 0.05
Assumptions: 1. The samples are both random and independent. 2. The samples are both normal since n>30 in both samples and this makes them normal according to C.L.T.
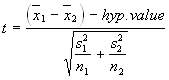
Two-sample T for Fall Weights vs Winter
Weights
N Mean StDev SE Mean
Fall
Weights 54 152.7 35.3 4.8
Winter Weights 44
153.0 36.9 5.6
Difference = mu (Fall Weights) -
mu (Winter Weights)
Estimate for difference: -0.34
95%
lower bound for difference: -12.54
T-Test of difference =
0 (vs >): T-Value = -0.05
P-Value = 0.518
DF = 90