Data            Graphs

Sampling and data collection:

To find our sample we compiled a list of every student enrolled in North Olmsted High School, which was 1,604 students.  Using MiniTab, we took a simple random sample of 160 students from our list.  Eight students that were randomly picked attend Polaris full time and therefore, could not be given the survey.  The population of interest is the entire student body at North Olmsted High School.  We did not block our sample in anyway.

Copy of the Survey

Of the 160 surveys, 126 were returned, but only 106 were adequately filled out.

Analysis and significance test:

We decided to use a one proportion z test because our data was dealing with a single proportion.

π = Given that the student carries their cell phone, the proportion who use it during school hours.

H₀:  π = 0.25

H_a: π > 0.25

Significance level: α =0.05

p= 0.5926

Assumptions:
n(π)>10 and n(1-π)>10
81(0.5926)=48
81(1-0.5926)=32.99

Test: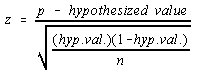  

N= 81

Z = 7.12065332

P-value: 5.407928 x 10^-13

Conclusion: We can reject our null hypothesis at any reasonable significance level because our p value is virtually zero.  Therefore, we have sufficient evidence to say that the proportion of students at North Olmsted High School who use their cell phones during the day is greater than 0.25.