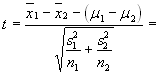Gender Maturity Among Teens

The Study:

 

We obtained our samples by using the random number generator to get the names of 75 males and 75 females. Then we went to the office to obtain the studyhall teachers of the selected students. If the student did not have a studyhall, we used their third period teacher since the students can complete the survey during the announcements. We then organized the teachers’ names alphabetically and also organized the names of the students for each teacher alphabetically to make it more convenient for the teachers. Our population of interest is the student body of North Olmsted High School. The sample mostly consists of males and females that attend North Olmsted High School full-time or part-time. The students that attend Polaris full time or PSEOP full time were not included in the sample.  

 

Survey:

Circle the best answer that applies to you!

1) What is your idea of a good time?

a. Sitting in the lounge, by the fire, doing absolutely nothing

b. Being on your own, doing what you want

c. Going out and meeting new people, soaking up culture

d. Reading or relaxing

e. Being pampered by family and friends

2) What is your favorite food?

a. Salads and health food

b. A varied selection of satisfying foods

c. Soup

d. Burgers, hot dogs, and fries

e. Candy, anything with loads of sugar!

3) How do you handle a situation?

a. Pure skill and experience

b. By using my age as an excuse

c. I really cannot be bothered

d. I use my sharp mind and a little technique

e. Someone else does it for me

4) Someone is breaking into your house. Do you:

a. Call the police right away, then hide

b. Hide in the closet until the coast is clear

c. Grab a baseball bat, after all, you can handle them yourself!

d. Wail and cry

e. Hope that your ears are not working properly

 5) Where do you go to have fun at night?

a. The mall

b. Museum, theater

c. I don’t, I play video games at home

d. Hang out at my friends’ house

e. Movies

6) Are you a female or a male?

a. Male

b. Female

Two-Sample T-Test and CI: Male Score, female score  
Descriptive Statistics: Male Score, Female score 

Variable        Mean  SE Mean  TrMean  StDev  Variance  Minimum  Median
Male Score    17.537    0.356  17.646  2.619     6.857    9.000  17.000
Female score  18.661    0.381  18.720  2.849     8.119   12.000  19.000

Variable      Maximum    IQR
Male Score     22.000  3.000
Female score   24.000  4.000

Summary of the counts:

 

Reflecting upon the statistics gathered from MINITAB, we can conclude that 

the average female score  exceeds the average male score by 1.124.  The 
standard deviation of the female sample studied is about  0.23 bigger than 
that of the male sample studied.  This comparison shows that there is a little
more variability within the female sample in terms of maturity.  The mean 
score for the male sample was affected by an outlier of 9, to slightly lower 
the mean.
 
Descriptive Statistics: Male Score, female score 

Variable      TrMean
Male Score    17.646
female score  18.720

Therefore, we conducted another trial of descriptive statistics to calculate the trimmed means of our samples.  From these results, we can conclude that the average female score is still higher than the  average male score.  After viewing 
the histograms of the study, we observed that the two graphs were both unimodal 
and slightly skewed to the left.  The boxplots of the study also confirmed these observations and clearly supported the presence of an outlier in the male sample. The boxplots also showed that the median of the female score is greater than the median of the male score.

 

The Significance Test

 

A two-sample t-test will be conducted because we are comparing two means without knowing the population standard deviation. The samples are independently selected random samples. Also, both the samples have a population greater than 30.

µ₁ = the true average male maturity “level” determined by the survey in North Olmsted High School

µ₂ = the true average female maturity “level” determined by the survey in North Olmsted High School

H_o: µ₁ = µ₂         (the average male maturity level is equal to the average female maturity level)

H_a: µ₁ != µ₂       (the average male maturity level is not  equal to the average female maturity level) 

α = 0.05  

We must assume:

    1. Both samples are independently selected random samples

    2. Both Populations are normally distributed since n1>30 and n2>30

Also, we don't know the population standard deviation, so we must use the t-test.

n₁ = 54, x₁ =17.54, s₁ =2.62 , n₂ =56, x₂ = 18.66, s₂ = 2.85 so,

t= [(17.54-18.66)-(17.54-18.66)]/√((2.62^2)/54)+((2.85^2)/56)

t= -2.15 and at 107 d.f. the p-value ≈ 0.033.

We can reject the null hypothesis at the 0.05 level of significance sine the p-value is less than α. Therefore, there is sufficient evidence to support the claim that the true average male maturity “level” is not equal to the female maturity “level” in North Olmsted High School.