The Study
Here you will find information about the study and how it was done. The results to the study are posted in Data.
The Mechanics of the Study...
The population of interest was all students at North Olmsted High School. The sample size for the survey was 72 students. This sample was obtained randomly. A list of all the students at the high school, stored in an excel file, was imported to Minitab under the “Surname” and “First Name” columns. In Minitab, using the random number generator, 72 students were randomly selected from these columns and placed in columns C10 and C11. The list was sorted by ascending alphabetical order of the last name. After obtaining the sample, the schedules of these students were procured and surveys were sent out to the students’ teachers.
Read on to see how the students cooperated...
The students...
The North Olmsted High School Students to whom surveys were sent out were fairly responsive. Fifty five students returned completed surveys out of a total of seventy two students who were sampled. Many responded immediately and the completed surveys were tallied right away. Thank you all who were kind enough to participate in my survey! You rock.
Survey...
Here is copy of my survey for those who were deprived of the opportunity to participate in this study. Have fun :)
Here are the descriptive statistics of the study:
Descriptive Statistics: BookAvg, MoviesAvg
BookAvg 48 0 2.479 0.217 1.504 0.000 1.000 2.357 3.536
MoviesAvg 48 0 4.187 0.170 1.181 1.714 3.429 4.214 4.857
BookAvg 6.000
MoviesAvg 7.286
From the statistics above, we get an inkling of what the results of a hypothesis test would be. The mean score for movies, 4.187, is higher than the score for books, 2.479. The median, minimum, maximum, first quartile, and third quartile values for movies are all greater than those for books. This led me to hypothesize that the true mean score for movies is greater than that for books. This is why the alternative hypothesis that stated that the books' score was less than the movies' score was used. Here is the hypothesis test.
Hypothesis Test
μd = the true mean difference between the approval score for books and movies
Ho: μd = 0
Ha: μd < 0
Significance level: α = 0.05
Assumptions: This sample is paired and it is selected randomly. The sample size is greater than 30. Hence, we can assume normality for this sample because of the Central Limit Theorem. Hence all of the assumptions for a paired t-test are met. Since we do not have the population standard deviation, we must use the t-test statistic instead of z.
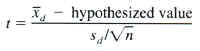
Paired T-Test and CI: BookAvg, MoviesAvg
BookAvg 55 2.379 1.536 0.207
MoviesAvg 55 4.166 1.254 0.169
Difference 55 -1.787 1.330 0.179
T-Test of mean difference = 0 (vs < 0): T-Value = -9.96 P-Value = 0.000
t = -9.96 with 54 degrees of freedom
P-value = 0.00
Conclusion: Since the p-value is less than α, we can reject the null hypothesis at the 0.05 level of significance. Therefore, there is sufficient evidence to support the claim that true mean difference between the approval score for books and movies is less than zero. Hence, the average approval score for books is less than the average approval score for movies for each person.