Recycling
Portland, Oregon vs. Cleveland, Ohio
The Study
Sampling Distribution
I first used Minitab to put simple numbers from 1 to
47 in the first column (Column C1) that I named
Numbers. I then hit
Calc>Random Data>Sample from Columns. I sampled 33 rows from the
Numbers column into a
separate second column, Places,
without replacement, to represent the 33 recycling centers that I would
contact. I had previously assigned each recycling center to a certain
simple number from 1 to 47, and now wrote the corresponding name of each
recycling center from the Places
column in column C3, labeled
Places_1. In the next columns in Minitab, labeled
Areacode and
Phonenumber, I put the area
code and phone numbers to the recycling center in the row, respectively.
I contacted each of these recycling centers and asked them to question
ten people at the recycling facility if they
do recycle at their own home.
Each of the recycling centers reported a sample proportion for how many
people in the recycling facilities in
Significance Test
I chose a one proportion z-test since I am only analyzing one proportion, which is proportion of recycling in Cleveland and because the assumptions are met to use a z-test.
π=the true
proportion of people that recycle all of their household materials in
![]() π=0.7
π=0.7
![]() π<0.7
π<0.7
α=0.05
Assumptions: Since pn>10 and n(1-p)>10, the data is normally distributed. The samples are independent and randomly chosen.
(0.7)(310)>10 217>10
(1-0.7)(310)>10 93>10
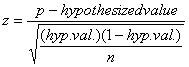
z critical value = -5.45
P-value=0
We reject the null hypothesis at any level of
significance since our p-value is 0. Therefore, we have sufficient
evidence to say that the true proportion of people that recycle all of
their household materials in
© Copyright 2009 | Design by Kumiko