Sampling
Starting with finding the sample size, we questioned 82 females and 73 males. Our population of interest is all males and females living in North Olmsted, Ohio who are above the age of 18. We randomly selected the people by selecting random streets of North Olmsted. To select the streets at random we put the streets of North Olmsted in a Minitab worksheet and number them accordingly. We then used a random number generator to select 7 random streets. The streets which were selected were; Hampton Drive, Edgepark Boulevard, Cottonwood Circle, Linwood Circle, Antler Drive, Colombia Road and Deerfield Drive. We then proceeded to ask every other house to question the residents who live there about their voter registration. To ensure that the samples were independent we only asked for the voter registrations of one gender within each household.
Significance Test
For this study, we chose to do a 2-proportion z-test because we had two
groups (males and females) and we were searching for the proportion of
males and females who were registered to vote within our sample. In our
study, we were trying to see if there was a difference between the two
proportions so we decided to use a not equal to alternative hypothesis.
Hypothesis:
π1 : The true proportion of males in North Olmsted, Ohio registered to
vote.
π2 : The true proportion of females in North Olmsted, Ohio registered to
vote.
Ho: π1 = π2
Ha: π1 ≠ π2
α = 0.05
Assumptions: Normal distribution, independent random sample, n(π) ≥ 10
and n(1-π) ≥ 10.
π1:
π2:
n(π) = 73(0.7808) = 56.9984 > 10
n(π) = 82(0.8537) = 70.0034 >10
n(1-π) = 73(1-0.7808) = 16.0016 > 10
n(1-π) = 82(1-0.8537) = 11.9966 > 10
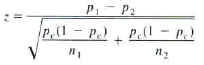
Test and CI for Two Proportions
Sample X N Sample p
1 57 73 0.780822
2 70 82 0.853659
Difference = p (1) - p (2)
Estimate for difference: -0.0728366
95% CI for difference: (-0.194731, 0.0490576)
Test for difference = 0 (vs not = 0): Z = -1.17 P-Value = 0.242
Fisher's exact test: P-Value = 0.297
z = -1.17
p-value: 0.242