Sampling Method
I obtained my sample when I was working my usual hours at Savory Sub, (Monday 4pm-8pm, Wednesday 4pm-9pm and Sunday 12pm – 8pm) throughout a period of two months. Each time that I worked, I recorded the gender and payment type of each take-out transaction. Deliveries and catered orders (bulk orders) were not included in this study, mainly because deliveries resulted in cash transactions while credit was used for catered orders. My sample was all of the take out customers who ordered pizza/sandwiches/sides from Savory Sub Cafe and Pizzeria. This included adults and children. Each transaction that was made was recorded on a slip of paper that was hanging in the restaurant. My population of interest is everyone who purchases food (pizza/sandwiches/sides) in store.
Hypothesis Tests
Credit
Π 1:
The proportion of men who use credit cards at Savory Sub Café and
Pizzeria
Π 2:
The proportion of women who use credit cards at Savory Sub Café and
Pizzeria
H0: Π 1=Π 2
Ha:
Π 1≠
α : .05
Assumptions:
Simple random samples and samples large; Π 1=82(0.550) >
10 and 82(1-.550) > 10 Π 2= 67(0.44966) >10 and 76(1-0.44966>10
Test
Statistic: 2 Proportion Z-Test
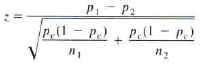
I will use
this test because there are two proportions that I wish to compare.
Pc= ((82)(0.550) + (67)(0.44966))/ (82+67)= 0.5049
Z = (0.550-0.44966)/
![]() = 1.75
= 1.75
p-value:
.0822365783
Π 1: The proportion of men who use cash at Savory Sub Café and Pizzeria
Π 2: The proportion of women who use cash at Savory Sub Café and Pizzeria
H0: Π 1= Π 2
Ha: Π 1≠ Π 2
α : .05
Assumptions: Simple random samples and samples large ; for Π 1 78(0.553) > 10 and 78(1-.553) > 10
And for Π 2 63(0.4468) > 10 and 63(1-0.4468) > 10
Test Statistic: 2 Proportion Z-Test
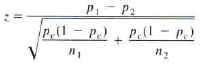
Pc = 78(0.553) + 63(0.4468) / 78+63 = 0.5055
0.553-0.4468 /
![]() = 1.8
= 1.8
p-value: 0.074
| Male Credit | Female Credit | Male Cash | Female Cash | Male Credit Prop | Female Credit Prop | Male Cash Prop | Female Cash Prop | |
| 82 | 67 | 78 | 63 | 0.550336 | 0.44966 | 0.55319 | 0.446809 | |