Does studying improve your ACT SCORE?

Sampling

My population of interest for this study is all students at North Olmsted High School that have taken the ACT. I took a random sample of 50 students from a list of all juniors and seniors (the grade levels that most likely already took the exam) using Minitab. After finding the names of the students, I looked up their schedules in the guidance office and the main office to determine what period the student would receive their survey and from what teacher. I then wrote that information along with the students’ names on separate post-it notes and stuck them to each survey. The surveys were then distributed to each teacher through their mailbox and then they gave them to their students. The survey I sent out was:

Have you taken the ACT?    Yes    No

If so, how many hours did you study for the exam?    _____

What was your composite score?   _____

*Remove the post-it note to insure confidentiality.

I’m using a two sample t-test for my data because I’m comparing two means and the population standard deviation is unknown so a z-test cannot be used.

u1= mean composite ACT score for students who studied

u2= mean composite ACT score for students who didn’t study

No: u1-u2= 0

Na: u1-u2> 0

a = .05

Assumptions: Random sample ✓, n≥30 so the Central Limit Theorem applies or appears normally distributed ✘

*Not all of the assumptions were met. Since my sample sizes are too small and the graphs don’t appear to be normal, I will continue the hypothesis test with caution. The results may not be valid.

 
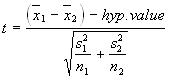
    t=  -0.5722

p-value=  0.7087 at 8.1658 df

Two-Sample T-Test and CI: Studied, DidntStudy

Two-sample T for Studied vs DidntStudy

            N   Mean  StDev  SE Mean

Studied     14  23.00   4.19      1.1

DidntStudy   6  24.33   5.01      2.0

Difference = mu (Studied) - mu (DidntStudy)

Estimate for difference:  -1.33

95% lower bound for difference:  -5.67